DOI: http://dx.doi.org/10.20986/revesppod.2023.1666/2023
RINCÓN DEL INVESTIGADOR
Cuestión de asociación: riesgo relativo y odds ratio (Parte II)
A question of association: relative risk & odds ratio (Part II)
Javier Pascual Huerta
Clínica del Pie Elcano. Bilbao, España
Recibido: 16-09-2022
Aceptado: 04-11-2022
Correspondencia: Javier Pascual Huerta
javier.pascual@hotmail.com
En el pasado número, en esta sección introdujimos los conceptos de riesgo relativo y odds ratio, muy comunes en la literatura médica actual. Estos valores, y especialmente el odds ratio, se utilizan en una gran cantidad de estudios para comparar el efecto de la asociación entre 2 variables binarias (por ejemplo, “sí” o “no”). A pesar de todo esto existe un problema con los odds: al revés que los riesgos, los odds son difíciles de entender. Debido a la controversia y malentendidos que generan en su interpretación clínica, hemos realizado una segunda parte para poder explicar su significado de forma más precisa.
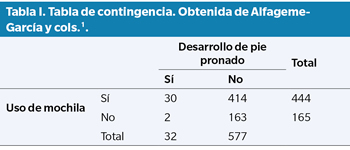
La Tabla I recoge los datos de un estudio de Alfageme-García y cols.1, publicado en 2020, sobre si el uso de mochilas podría ser un factor de riesgo para el desarrollo de un pie pronado durante la edad infantil. Hicieron un estudio prospectivo durante 3 años en los que estudiaron la aparición de pies pronados en niños que habitualmente usan mochilas y niños que habitualmente no las usan. El odds radio lo calculamos dividiendo el odds de desarrollar pie pronado en niños que usan mochila (30/414 = 0.072) entre el odds de desarrollar pie pronado en niños que no usan mochila (2/163 = 0.0122), es decir, 0.072/0.0122 = 5.9. Estos resultados del odds ratio indican que existe una asociación positiva entre el uso de mochila en edad infantil y el desarrollo de pie pronado. El IC al 95 % para dicho odds ratio va desde 1.39 a 24.99. Es decir, es un resultado estadísticamente significativo para una prueba de contraste de hipótesis al 5 % (valor p menor de 0.05), ya que el intervalo de confianza no cruza el valor de 1.0.
En definitiva, según este estudio, el uso de mochilas en la edad infantil es un factor de riesgo de desarrollar un pie pronado. Ese riesgo es de 5.9 odds más para niños que usan mochilas que para niños que no las usan. Pero, ¿qué significa esto desde el punto de vista clínico? Un odds de 5.9 no significa que haya un riesgo 5.9 veces mayor. El odds ratio no se interpreta en términos de probabilidad sino en términos de odds. Un odds ratio de 5.9 significa que si de 100 niños que no usan mochilas esperaríamos en condiciones normales que 1 de ellos desarrollara pie pronado, entonces de 100 niños que usan mochilas esperaríamos que 7 niños desarrollaran pie pronado (aproximadamente 1 + 5.9) (Figura 1).

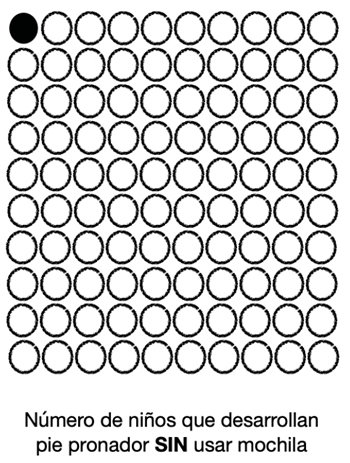
Figura 1. Gráfica del número de niños que desarrollarían pie pronado con y sin usar mochila según los datos de Alfageme y cols.1.
Los autores en el artículo utilizaron como estadístico únicamente el odds ratio y no el riesgo relativo que nosotros podemos calcular con los datos de la tabla de contingencia que hemos extraído del artículo. La proporción de niños que desarrollaron un pie pronado y que usaban mochilas es 30/444 = 0.067 (6.7 %) y la proporción de niños que desarrollaron un pie pronado y que no usan mochila es de 2/165 = 0.012 (1.2 %). El riesgo relativo (ratio de proporciones) sería de 0.067/0.012 = 5.58. Este valor de riesgo relativo es mucho más intuitivo clínicamente. Se puede expresar de varias formas y significa que el riesgo de desarrollar pie pronado aumenta en edad infantil 5.58 veces al usar mochilas con respecto a no usarlas a los 3 años. Si en una población esperaríamos que un 10 % de los niños que no usan mochilas desarrollara pie plano, el uso de mochila aumentaría esa proporción a 10 × 5.58 = 55.8 %.
Este ejemplo de Alfageme y cols. nos muestra que existen 2 problemas con el uso de odds ratio en los estudios. El primer problema es que odds ratio es intuitivamente difícil de entender para los clínicos. Intentar explicar a tu paciente, a tu compañero podólogo o incluso a ti mismo qué demonios significa un odds ratio de 5.9 no es sencillo. Por contra, es mucho más fácil para los clínicos coger el concepto y la relevancia clínica del riesgo relativo. Este caso concreto de Alfageme-Garcia y cols. es especial porque el valor de odds ratio y riesgo relativo se aproximan bastante (5.9 vs. 5.59). Bajo determinadas circunstancias, odds ratio y riesgo relativo tienen valores muy similares, especialmente cuando la probabilidad de que ocurra un evento es baja (menor de un 10 %), que es lo que pasa en el estudio de Alfageme y cols., ya que la probabilidad de desarrollo de pie pronado es menor del 10 % en ambos grupos. Pero cuando un evento ocurre de forma más común, el odds ratio aumenta dramáticamente y se separa mucho del riesgo relativo. Si imaginamos hipotéticamente que en el estudio de Alfageme y cols. el riesgo de desarrollar pie pronado en niños que no usan mochila no fuera de un 1.2 % sino de un 15 % (25 casos de 165 en vez de 2 casos de 165) un riesgo relativo de un 5.58 implicaría un número de casos de desarrollo de pie pronado en el grupo de niños que usan mochila de 375 casos, lo que daría un valor de odds ratio de 31.9.
El segundo problema es que el comportamiento similar del riesgo relativo y del odds ratio respecto al valor 1.0 para estudiar un factor de riesgo, y el hecho de que cuando el evento no es común los valores sean muy similares, hace que muchas veces se usen como valores sinónimos o intercambiales. Así, odds ratio es inapropiadamente interpretado como si fuera la misma cosa que el riesgo relativo. Los odds ratio siempre sobrestiman el valor de riesgo relativo pero su interpretación es diferente. Tiene que realizarse no en términos de probabilidad sino en términos de odds.
Los odds ratio son complicados de entender. Entonces, ¿por qué los usamos constantemente para describir resultados en vez de otro tipo de variables más simples o intuitivas, como el riesgo relativo? Existen varios motivos. Primero, odds ratio se puede utilizar en una amplia variedad de estudios (cohortes, casos y controles, transversales, ensayos clínicos, y metanálisis entre otros). Segundo, tiene propiedades matemáticas muy buenas que hace de ella una prueba robusta. Supongamos que miramos a la tabla ahora desde el otro lado y preguntamos ¿cuál es la probabilidad de que los niños con pie pronado usen mochilas? La probabilidad es 30/32 (93.7 %) y el odds 30/2 = 15. Para un niño sin pie pronado la probabilidad de usar mochila es 414/577 (71.75 %) y el odds 414/163 = 2.53. El riesgo relativo de esta manera sería 93.7/71.7 = 1.31 y el odds ratio 15/2.53 = 5.9. El odds ratio es el mismo, independientemente de la manera que hagamos el cálculo (el riesgo relativo no). Si cambiamos el orden de las columnas y filas, obtenemos el mismo odds ratio. Si cambiamos el orden solo de las columnas o solo de las filas, obtenemos el recíproco del odds ratio (1/5.9 = 0.17). Tercero, odds ratio permite examinar el efecto de otras variables en la asociación, permitiendo realizar ajustes a su valor, especialmente cuando se usa haciendo regresión logística. De hecho, en el estudio de Afáneme-García y cols. los autores realizaron un ajuste del valor del odds ratio por medio de regresión logística multivariable en el que se tuvieron en cuenta otras variables como sexo, IMC, sedentarismo o tipo de calzado utilizado, y que ajustó el valor del odds ratio a 6.44 (IC al 95 %: 1.49-27.82). Estos factores hacen del odds ratio un indicador muy útil desde el punto de vista estadístico de la asociación entre 2 variables por lo que, en definitiva, seguiremos usando odds ratio por mucho tiempo.

Bibliografía
Bibliografía recomendada